Spulenformel von K1PLP aus der QST

In der QST, der Mit­glied­er­zeit­schrift der ARRL, wurde 1974 von K1PLP eine Formel für die In­duk­ti­vi­tät der Ver­läng­er­ungs­spule an­ge­ge­ben [K1PLP]. Sie ist in Zoll und Fuß dimen­sio­niert und verlangt für beide Teil­strah­ler den selben Durch­mes­ser. Auf den ersten Blick unter­schei­det sie sich deutlich von der von mir her­ge­lei­tet­en Formel. Wenn man aber genauer hinsieht, erkennt man, daß beide Fromeln im Prinzip gleich sind. Die Formel aus der QST ist nur — wohl auch als Zu­ge­ständ­nis zum damals noch üblichen Rech­en­schie­ber — ver­ein­facht und gerundet. Da die Formel immer wieder zitiert wird und auch auf anderen Web­seiten für Online-Rechner heran­gezogen wird, habe ich mir mal die Mühe gemacht, sie abzuleiten.

Herleitung

Die In­duk­ti­vi­tät der Ver­läng­erungs­spule wird wie folgt angegeben:

Dabei ist A die Gesamt­länge des Dipols in Fuß, B die Länge des gespeisten Strahlers in Fuß und D der Durch­messer des Strahlers in Zoll, der auf beiden Seiten der Spule gleich groß ist. Das folgende Bild zeigt die hier verwendeten Abmessungen.

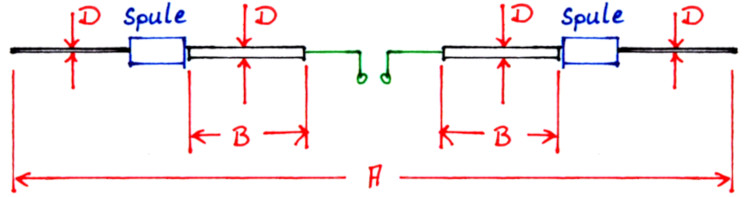
Die Herleitung der Formel geschieht grund­sätz­lich auf dem selben Wege wie zuvor. In den Aus­gangs­gleich­ung­en besteht aller­dings der Unter­schied, daß ein anderer Wellen­wider­stand herangezogen wird, nämlich

Diese Gleichung finded sich indirekt in [Ellingson], Gleichung (10.4.1). Im [Rothammel], Gleichung (4.3.6), ist anstelle von D der Radius gefragt, die Bedeutung von l ist nicht klar (Dipol­arm oder ganzer Dipol?). In [K3OQF] ist die Gleichung auch genannt, hier sind die Länge eines Dipol­arms und der Radius gemeint. Leider fehlt mir der Zugang zur Ori­ginal­lit­eratur.

Mit dem geänderten Wellen­wider­stand folgt man nun dem Rechenweg aus dem Spulen­rechner. Dabei ist zu beachten, daß das entfernte Stück in der neuen Nomen­kla­tur die Länge l_x = λ/4 - B hat und die nach der Spule angefügte Spitze die Länge A/2 - B. Die Induk­tivi­tät der Ver­läng­er­ungs­pule ergibt sich also zu

Das sieht dem gesuchten Ausdruck nur zum Teil ähnlich — vor allem ein Kotangens kommt in der QST-Formel gar nicht vor. Nun ist die QST-Formel zu einer Zeit veröffentlicht worden, als der Rechenschieber noch Standard war. Einen Kotangens auszurechnen, und dann auch noch im Bogenmaß (Tri­gono­met­rische Funktionen waren üblich­er­weise in Grad angegeben), war sicher kein Spaß. Also ist der Kotangens genähert worden. Es gilt:

Diese Näherung wird nun angewendet, wobei die –1 von vor der Klammer kommt. Es ergibt sich

und nach etwas aufräumen

An dieser Stelle kann mit c₀ = λ·f schon mal im Vor­fak­tor der Term π² f² her­aus­ge­ar­bei­tet werden.

Jetzt kommt eine Rundung, die vielleicht etwas weh­tut. Der Term 2π/√3 ist 3,63…, das ist — Augen zu und druch! — etwa 4. Im linken Term steht 2π/√3 · ¼, das ist 0,91…, also etwa 1. Obwohl der Fehler hier genauso groß ist, sieht es nicht ganz so schlimm aus. Nachdem wir uns von dem Schreck erholt haben, können wir uns am schönen Ergebnis erfreuen.

Jetzt soll der Übergang von einer Größen­gleich­ung zu einer Zahlen­wert­gleich­ung in mittel­alter­lichen ameri­ka­nischen Einheiten stattfinden. Man beachte, daß ein Fuß einer Länge von zwölf Zoll entspricht.

Besondere Auf­merk­sam­keit verdient die Wellen­länge λ. Hier ist immer die Wellen­länge auf dem Anten­nen­draht gemeint, also wird sie mit dem Kor­rek­tur­faktor k = 0,95 multi­pli­ziert. Außerdem soll die Wellen­länge durch die Frequenz aus­ge­drückt werden. Dabei wird die Licht­ge­schwind­ig­keit natürlich in Fuß eingesetzt, also 948·10⁶ Fuß/s. Da die Wellen­länge in der Formel nur noch als λ/4 vorkommt, ist auch nur dieser Wert angegeben. Der Voll­stän­dig­keit halber soll erwähnt werden, daß diese Ersetz­ung nicht ganz sauber ist. Ein λ hat sich schon in den Vorfaktor als 1/f ver­ab­schie­det und bekommt jetzt keinen Kor­rek­tur­fak­tor mehr.

Auch hier kann natürlich kräftig aufgeräumt werden. Es ergibt sich

Wird ε₀ eingesetzt, kol­la­biert der erste Bruch — liebevoll gerundet — zu 1/68. Dann müssen die Brüche im Klam­mer­aus­druck nur noch leicht zu­recht­ge­rückt werden, und man erhält die Formel aus [K1PLP].

Vergleich

Zuletzt sollen die Formel aus der QST mit der Her­lei­tung auf Basis des Meinke-Gund­lach ver­glich­en werden. Dazu wird die In­duk­ti­vi­tät für eine Antenne für das 10-m-Band bei f = 29 MHz berechnet. Die Spule soll genau in der Mitte sein, es ist also l₁ = l₂ oder A/2 = 2 B. Der Anten­nen­stab soll überall einen Durch­messer von 2 mm haben, es ist also d₁ = d₂ = D = 2 mm.

Im folgenden Bild ist die Induk­ti­vi­tät für ver­schie­dene Be­rech­nungs­va­ri­an­ten gezeigt.

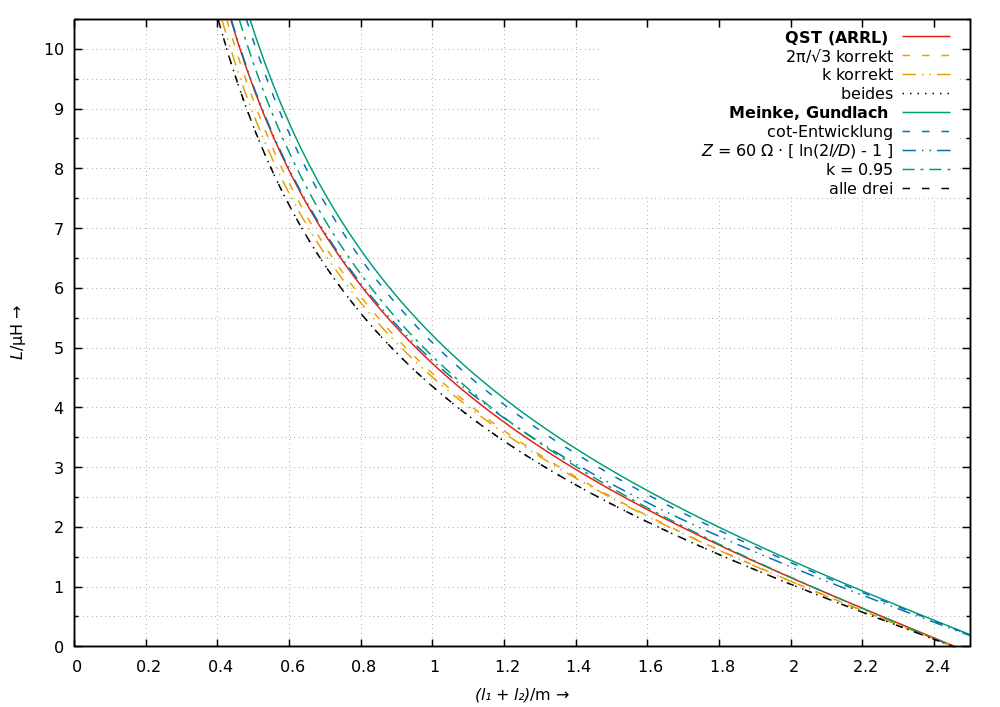
Varianten der QST-Formel

QST (ARRL) Das ist die Formel aus der QST, wie sie hier diskutiert wird.

2π/√3 korrekt Diese sehr grobe Näherung, die letz­ten­en­des den Ko­tan­gens ver­fälscht, wird nicht gemacht.

k korrekt Der Kor­rek­tur­fak­tor wir auch im Vor­fak­tor ein­ge­rech­net, obwohl sich die Wel­len­län­ge dort schon als f „versteckt“ hatte.

beides Anwendung beider Mo­di­fi­ka­tion­en der QST-Formel. — Die Formel entspricht jetzt genau der Meinke-Gundlach-Formel mit allen Mo­di­fi­ka­tion­en.

Er­staun­lich­erweise bewirken die beiden groben Rund­ungen, die bei der Her­lei­tung der QST-Formel gemacht wurden, daß die Werte sich der Meinke-Gundlach-Formel annähern.

Varianten der Meinke-Gundlach-Formel

Meinke, Gundlach Formel, wie sie sich ohne Klim­mzüge aus den Grund­gleich­ung­en ergibt (Her­lei­tung im Spulen­rechner). Ins­be­son­dere wird kein Kor­rek­tur­fak­tor ver­wen­det, es gilt also k = 1.

cot-Entwicklung Der Kotangens wird, wie in der QST-Formel, durch die ersten beiden Glieder seiner Reihen­ent­wick­lung ersetzt. — Die Ent­wick­lung des Kotangens hat nur einen sehr kleinen Einfluß auf die er­rech­nete In­duk­ti­vi­tät. Damit ist gezeigt, daß die Näherung legitim ist.

Z = 60 Ω · [ ln(2l/D) - 1 ] Es wird der gleiche Wel­len­wi­der­stand wie in der QST-Formel verwendet.

k = 0,95 Der Kor­rek­tur­fak­tor von 0,95 wird be­rück­sicht­igt. Genau so wird die Formel im Spulen­rechner verwendet.

alle drei Alle drei Mo­di­fi­ka­tion­en der Meinke-Gundlach-Formel. — Die Formel entspricht jetzt genau der QST-Formel ohne grobe Rund­ung­en.

Für den Fall, daß keine Ver­läng­erungs­spule benötigt wird, wenn also die Ge­samt­län­ge der Antenne gleich λ/4 wird, liefern alle Formeln den korrekten Wert L = 0. Die ge­rech­net­en Varianten teilen sich dann in die beiden Gruppen k = 1 und k = 0.95 auf.

Literatur

[Ellingson] Steven W. Ellingson: “Reactance of the Electrically-Short Dipole.”, 22. March 2021. Retrieved 11. April 2021, from ↥https://eng.libretexts.org/@go/page/19608

[K1PLP] Jerry Hall, K1PLP: “Off-Center-Loaded Dipole Antennas”, QST, Sep 1974, pp. 28–35, 58

[K3OQF] Walter Schulz: “Designing a Vertical Antenna”, QST, Sep 1978, pp 19–21

[Meinke-Gundlach] H. Meinke, F. W. Gundlach: „Taschen­buch der Hoch­fre­quenz­tech­nik“, 3. Auf­la­ge, Springer-Verlag, Ber­lin/Hei­del­berg/New York, 1968

[Rothammel] Alois Kirschke, DJ0TR: „Rot­ham­mels An­ten­nen­buch“, 13. Auf­la­ge, DARC Ver­lag, Bau­na­tal, 2013