Spulenrechner

Bemaßung

Dieser Spulenrechner dient dazu, Ver­läng­erungs­spulen für λ/2-Dipole oder λ/4-Ver­tikal­strah­ler zu berechnen. Die Bemaßung der Anten­nen­drähte ist in der folgenden Abbildung dargestellt.

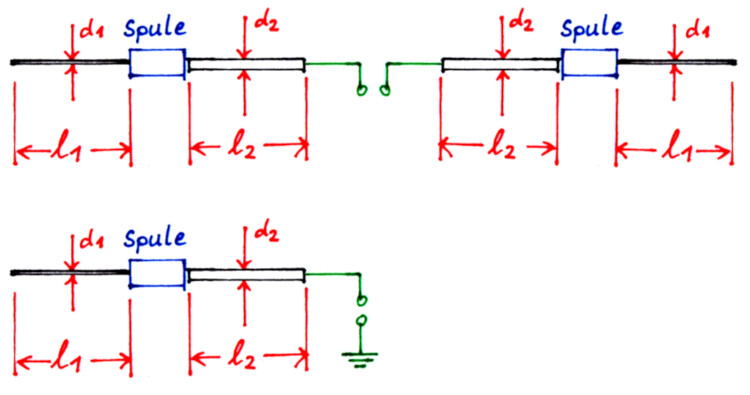
Für den Fall, daß die Spulen als Zylin­der­spulen ohne Kern ausgeführt werden, folgt gleich im Anschluß ein weiterer Rechner. Sollen die Spulen als 1,5-mm²-Instal­lations­draht auf HT-Rohr gewickelt werden, können die Maße gleich vor­ein­ge­stellt werden. Dabei werden die zusätz­lichen Längen­maße der Wand­stärke des HT-Rohrs und der Iso­lierung der Instal­lations­drahtes gleich mit­berück­sich­tigt. Sollen andere Abmes­sungen verwendet werden, können die Maße anhand der folgenden Skizze in den Rechner eingetragen werden.

Als Bonus gibt der Spulen­rechner auch noch die Gesamtlänge l_Dr des Spulen­drahtes an. Aber Vorsicht, es handelt sich nur um die Länge der reinen Windungen ohne Anschlüsse und auch ohne Reserve für ein bis zwei zusätz­liche Windungen zum Abgleich.

Rechner

Induktivität

l₁ = m l₂ = m

d₁ = mm d₂ = mm

f = MHz

L =

—

µH

Berechnung der Spule

Abmessungen

freie Auswahl

1,5 mm² auf HT 40

1,5 mm² auf HT 50

1,5 mm² auf HT 75

D = mm

d = mm a = mm

L = µH

berechnen

übernehmen

w = Wdg.

berechnen

l_Dr =

—

m

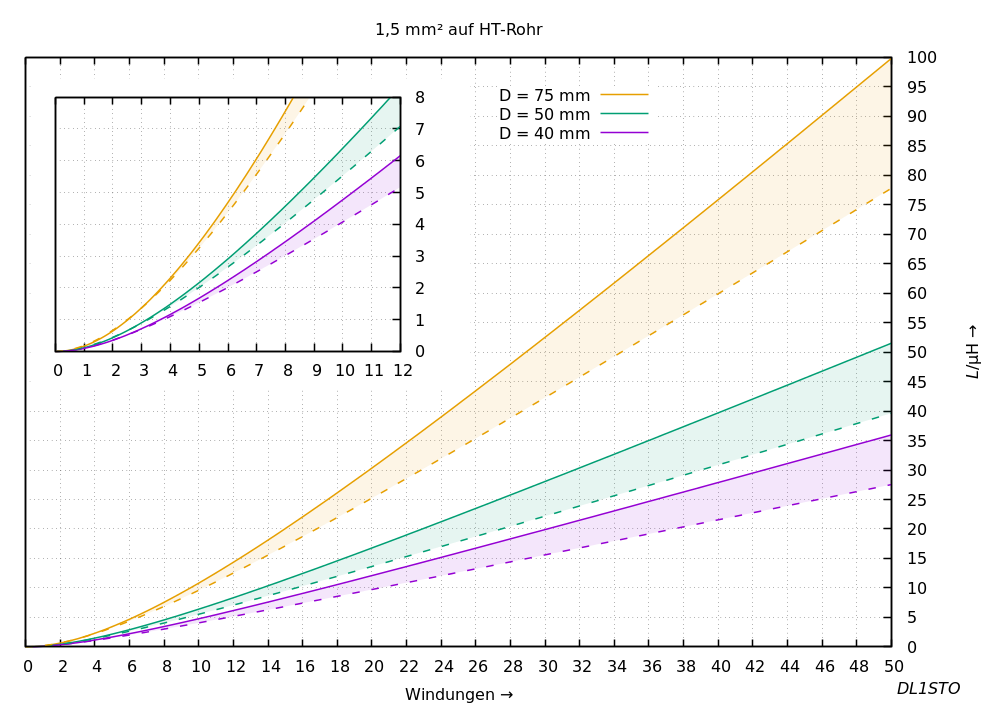
Das fol­gen­de Dia­gramm ver­mit­telt einen schnellen Über­blick über die Dimen­sion­ier­ung der Zylin­der­spulen. Der farbig schat­tierte Bereich markiert den Fehler, der sich ergibt, wenn bis zu 1 mm Win­dungs­ab­stand zu­sätz­lich zur Kabel­iso­lier­ung besteht.

Berechnungsformeln

Die dem Rechner zu­grun­de­lie­gen­den Formeln sind aus Grund­gleich­ungen aus [Meinke-Gundlach] abgeleitet.

Induktivität der Verlängerungsspule

Um die Induk­tivität einer Ver­läng­erungs­spule zu berechen, stelle man sich zunächst einen voll­stän­dingen λ/4-Strahler (bzw. eine voll­stän­dige Hälfte eines λ/2-Dipols) vor. Dieser Strahler hat eine Länge von k·λ/4, wobei k der Ver­kür­zungs­fak­tor ist und üblich­er­weise einen Wert von 0,95 hat. Als nächstes wird dieser voll­stän­dige Strahler auf die Länge l₂ gekürzt. Das abge­schnitt­ene Stück hat die Länge l_x, wie im folgenden Bild zu sehen.

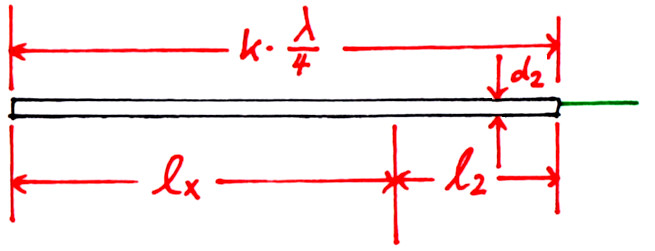
Das fehlende Stück l_x betrachten wir jetzt als kurzen Strahler, dessen Fuß­punkt­reaktanz X_F,x wir aus­rech­nen wollen. Diese Reaktanz X_F,x ist es nämlich, die wir an l₂ an­schlie­ßen müssen, um wieder einen reso­nanten Strahler zu erhalten. Da X_F,x zu kurz ist, um resonant zu sein, erwarten wir eine negative Reaktanz, also ein kapa­zitives Verhalten.

Im Kapitel „H. Antennen“ in [Meinke-Gundlach] finden sich die nötigen Formeln. Die Fuß­punkt­reak­tanz eines Stabes wird in (17.10) angegeben mit

Dabei sind l die Länge des Stabes, λ die Wel­len­länge und Z_A der Wel­len­wi­der­stand auf dem Stab. Letz­ter­er wird in (17.9) an­ge­ge­ben mit

was eigentlich

heißen soll. Darin ist l wieder die Länge des Stabes und D sein Durch­messer. Wenn mir jemand sagen kann, woher der Faktor 1,15 kommt, wäre ich sehr dankbar!

Hinweis: Die Formeln H(17.9) und H(17.10) aus dem [Meinke-Gundlach] findet man auch als (4.3.5) und (4.1.3) im [Rothammel].

Die gesuchte Fuß­punkt­reak­tanz X_F,x ist damit also bekannt:

Dabei habe ich mir erlaubt, 1/tan als cot zu schreiben.

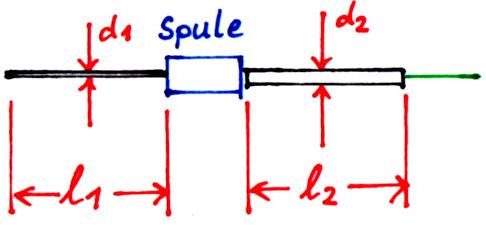
Der entfernte Teil­stab mit der Länge l_x wird durch einen kürzeren Stab der Länge l₁ ersetzt, wie im Bild oben zu sehen. Dessen Fuß­punkt­reak­tanz ist

Es haben sich nur die Länge (jetzt l₁) und der Durch­messer (jetzt d₁) des Stabes geändert. Die Differenz der beiden Fuß­punkt­reak­tanzen muß durch ein Bauteil ersetzt werden. X_F,x und X_F,1 sind beide negativ, da ja beide Stäbe für sich genommen zu klein für die Wellen­länge, also kapa­zitiv sind. X_F,1 ist jedoch betrags­mäßig größer, da dieser Stab kleiner ist, also weiter weg von der passenden Länge ist und somit die größere Kapazität zeigt. Der Ausdruck

ist also positiv — das gesuchte Bauteil mit der Reaktanz ΔX ist also eine Spule. Die Induk­tivi­tät L der Spule kann leicht aus­ge­rech­net werden, wobei die Spulen­reaktanz X_L der gesuchten Reaktanz ΔX entspricht:

Von dieser Formel für L ausgehend können wir alle Größen einsezten:

Um die Formel praxis­taug­lich zu machen, sind noch zwei Dinge zu beachten. Zum einen ist mit der Wellen­länge λ die Wellen­länge auf dem Stab gemeint; es muß also der Ver­kürz­ungs­fak­tor k berück­sichtigt werden, so daß gilt: λ = k · c₀ / f. Zum anderen kommt die Länge l_x in der fertigen Antenne über­haupt nicht mehr vor. Sie soll also direkt durch die Länge l₂ aus­ge­drückt werden: l_x = k · λ/4 – l₂ = ¼ · k · c₀/f – l₂. Mit diesen beiden Er­setz­ungen ergibt sich für die gesuchte In­duk­tivi­tät der Spule der schöne Ausdruck

Zylinderspule

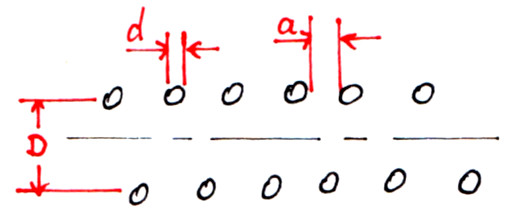
Die Formel für die Zylin­der­spule stammt aus dem Kapiel „A. Bau­ele­mente“ in [Meinke-Gundlach]. Für eine ein­lagige Zylin­der­spule mit der oben gezeigten Bemaßung wird für l > 0,3 D und a/d < 4 in den Formeln (5.3) und (5.4) der Wert

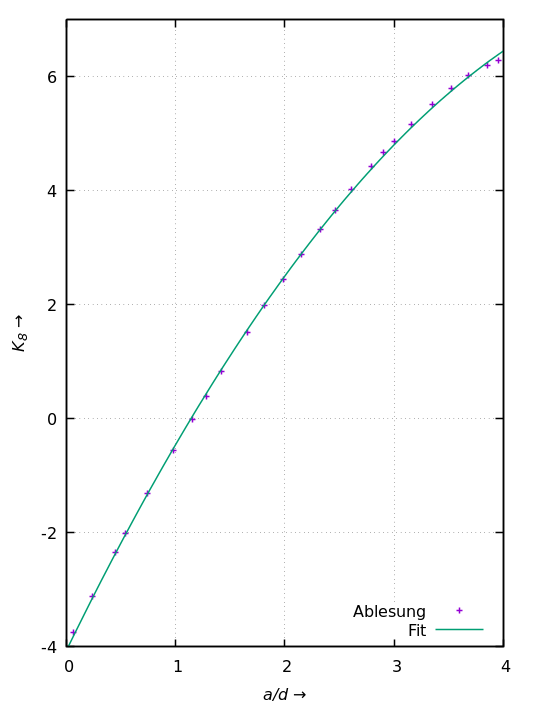
angegeben. Die Länge l der Spule ergibt sich zu l = (w – 1)·(a + d). Der Kor­rek­tur­fak­tor K₈ muß aus einem Dia­gramm abgelesen werden. Ich habe einige Werte aus dem Dia­gramm abgelesen und benutze zur Berechung von K₈ die best­approx­imier­ende Parabel, die im folgenden Graphen zu sehen ist.

Literatur

[Meinke-Gundlach] H. Meinke, F. W. Gundlach: „Taschen­buch der Hoch­fre­quenz­tech­nik“, 3. Auf­la­ge, Springer-Verlag, Ber­lin/Hei­del­berg/New York, 1968

[Rothammel] Alois Kirschke, DJ0TR: „Rot­ham­mels An­ten­nen­buch“, 13. Auf­la­ge, DARC Ver­lag, Bau­na­tal, 2013